
| Главная |
| Поиск по сайту |
| Полезные ссылки |
| Главная |
| Поиск по сайту |
| Полезные ссылки |
<<Предыдущая страница Оглавление книги Следующая страница>>
РАБОТА С КАРТОЙ
При работе с топографической картой приходится измерять расстояние по прямой линии, по извилистой, а также измерять и вычислять углы. Для этого необходимо прежде всего знать масштаб карты.
Масштабом называется отношение длины линии на карте к длине соответствующей линии на местности, выраженное в одинаковых мерах длины. Различают численные и линейные масштабы карты.
Численный масштаб записывается в виде дроби или отношения двух чисел. В числителе стоит единица, а в знаменателе — число, которое показывает, во сколько раз действительные размеры на местности уменьшены при изображении на карте, например:
1/10 000 или 1 : 10 000.
Число 10 000 показывает, что все расстояния на местности уменьшены в 10 000 раз.
Для определения по карте расстояния между местными предметами пользуются численным масштабом. Для этого измеряют линейкой или циркулем расстояние между местными предметами в сантиметрах и умножают полученное число на величину масштаба.
Например, если на карте масштаба 1 : 25 000 расстояние между двумя точками равно 5,5 см, то расстояние на местности будет равно 5,5X250=1375 м.
Для определения небольших расстояний между двумя точками проще пользоваться линейным масштабом.
Линейный масштаб — это графическое изображение численного масштаба (рис. 7). Он представляет собой прямую линию, разделенную на отрезки равной длины, называемую основанием линейного масштаба. Основание выбирается с таким расчетом, чтобы ему на местности соответствовало круглое число сотен или тысяч километров. Если есть необходимость построить линейный масштаб для карты масштаба 1:50 000, то за основание лучше принять отрезок 2 см. Тогда каждому такому отрезку на местности будет соответствовать расстояние 1 км. Если нужно измерить линию, меньшую, чем длина основания, то основание делят еще на 5—10 равных частей.
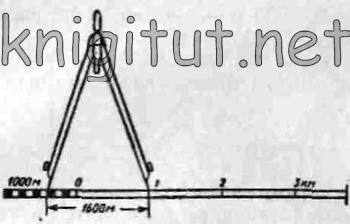
Рис. 7
Поскольку линию на карте точно измерить нельзя, то расстояния на местности 10 и 50 м, соответствующие 0,01 см на карте, показываются предметной точностью масштаба карты. Практически ошибка измерения линий па карте в полевых условиях составляет 0,05 см и более.
В практике туризма часто приходится пользоваться картами неметрических масштабов или фотокопиями карт произвольного масштаба.
Чтобы с такой картой можно было работать, необходимо построить переводной линейный масштаб.
Например, сделана фотокопия карты масштаба 1:300 000. Масштаб фотокопии получится равным 1 : 387 865. Если построить линейный масштаб с основанием 1 см, то в натуре ему будет соответствовать 3878,65 см. Это создает определенные трудности в работе с таким масштабом. Удобнее построить такой линейный масштаб, основанию которого в натуре соответствовало бы круглое число километров или сотен метров, например 5000 м. Длину такого основания находим из следующей пропорции: 1 см: x: см = = 3878,65:5000 м; х=5000/3378,65 =1,29 см.
На крупномасштабных картах часто приходится определять координаты точек.
Координатами точек называют угловые или линейные величины, характеризующие положение точек на поверхности или в пространстве. Для определения координат точек пользуются координатной меркой (рис. 8).
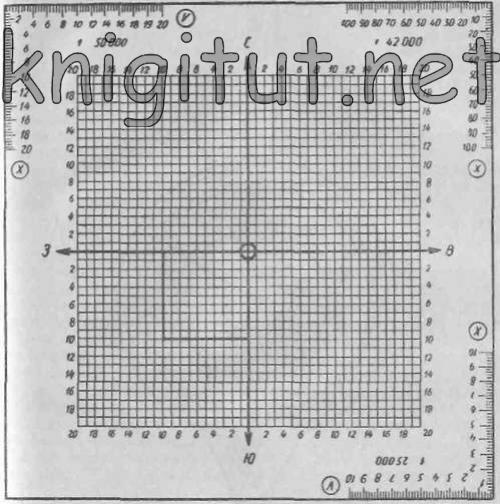
Рис. 8
Координатная мерка— это прозрачная целлулоидная пластинка с координатной сеткой. Две взаимно перпендикулярные линии делят координатную сетку на четыре равных квадрата; эти линии оканчиваются стрелками, имеющими обозначения: С (север), Ю (юг), З (запад), В (восток). Расстояние между линиями сетки равно 2 мм; цена деления сетки для карт масштабов 1 :25 000 и 1 :50 000 соответственно равна 50 и 100. В северо-восточной части сетки выделены жирными линиями квадраты со сторонами в 2 см.
На углах пластинки имеются шкалы, служащие для определения координат точек карты при разных ее масштабах. Шкалы для масштабов 1:25 000 и 1:50 000 имеют миллиметровые деления и оцифрованы в сотнях метров; шкала для масштаба 1 :42 000, оцифрованная через 0,2 дюйма, предназначается для старых карт, разграфленных на дюймовые и двухдюймовые квадраты. В центре пластинки имеется отверстие для накола точек при нанесении их на карту.
Координатометр имеет вид угольника, на внутренних сторонах которого нанесены миллиметровые деления, оцифрованные в сотнях метров.
Если расстояние между штрихами делений равно 2 мм, то цена деления для карт масштабов 1 :25 000 и 1 :50 000 соответственно равна 50 и 100 м.
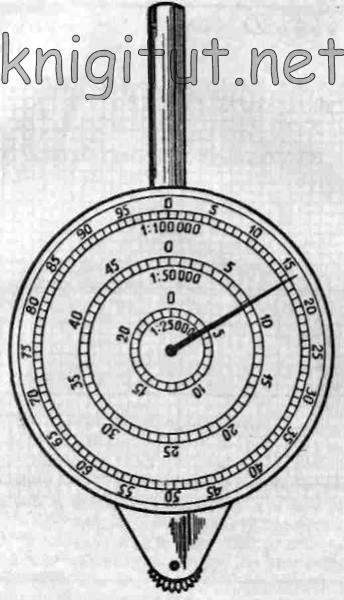
Рис. 9
Измерение расстояний по ломаной линии производится с помощью циркуля или курвиметра. При пользовании циркулем створ его делают небольшим в зависимости от степени извилистости измеряемого расстояния.
Курвиметр имеет вид круглой коробочки с держателем (рис. 9). В центре прибора находится циферблат со стрелкой, внизу имеется колесико, при помощи которого обводится маршрут. Колесико соединено системой передач со стрелкой на циферблате, которая ведет отсчет величины пройденного расстояния по карте.
Деления на шкале циферблата курвиметров бывают различные: на одних курвиметрах они обозначают путь, проходимый колесиком по карте в сантиметрах, на других —показывают непосредственно расстояние на местности в километрах в зависимости от масштаба карты. На рисунке показан курвиметр с тремя шкалами различных масштабов (1: 100000, 1:50000, 1:25000). Деления на шкалах показывают расстояние на местности в километрах.
Чтобы определить длину маршрута с помощью курвиметра, необходимо стрелку прибора установить на нулевое положение циферблата. Затем курвиметр следует поставить вертикально колесиком на начальную точку маршрута и с равномерным нажимом прокатить его вдоль маршрута так, чтобы показания стрелка возрастали. В конечной точке маршрута снимают отсчет по нужной шкале циферблата. Длина маршрута будет равна отсчету, умноженному на цену деления шкалы.
Если курвиметр дает показания в сантиметрах, то для получения соответствующего им расстояния на местности необходимо умножить отсчет по шкале на величину масштаба карты.
Но точно измерить расстояние по линейному масштабу невозможно, так как делить его основание на очень мелкие части нельзя. Это затрудняет отсчет.
Для большей точности измерений следует применять так называемый поперечный масштаб.
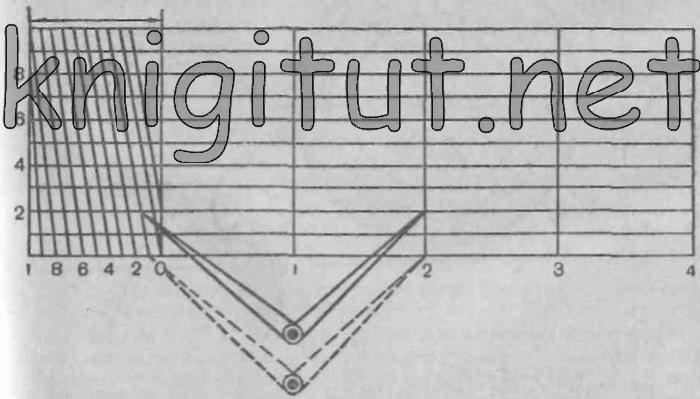
Рис. 10
Поперечный масштаб (рис. 10) представляет собой прямоугольник, горизонтальная сторона которого разделена на несколько равных частей, обычно по 2 см каждая. Каждая часть носит название основания масштаба. Крайнее левое основание в верхней и нижней частях поперечного масштаба делится на 10 равных частей. Концы этих десятых долей основания соединяются между собой прямыми, отсекающими на горизонтальных линиях сотые доли основания. Таким образом, на поперечном масштабе измеряемое расстояние может быть выражено в целых, десятых и сотых долях основания масштаба. Зная величину основного масштаба (2 см), можно определить «цену» основания в метрах.
Так, для масштаба 1:25 000 «цена» основания поперечного масштаба составляет 500 м, его десятая доля — 50 м, а одна составная часть — 5 м. Поперечным масштабом пользуются так. Циркулем измеряют расстояние между двумя предметами на карте. Затем прикладывают циркуль к нижней линии поперечного масштаба и отсчитывают расстояние, получается 2200 м с излишком. Чтобы определить этот излишек, необходимо циркуль передвигать параллельно нижней линии вверх до пересечения с диагональю и считать окончательную величину расстояния 2200 м.
return_links(); ?>